Sinus och Cosinus
I många sammanhang när man programmerar stöter man på en funktion som
heter sin(), eller sinus. Vanligtvis
används denna funktion för beräkningar på cirklar och liknande
figurer, men den kan också användas till lite roligare beräkningar
för grafiska ändamål.
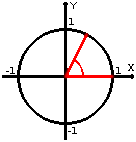
Vi ska börja med att studera figuren ovan, den så kallade
enhetscirkeln. Det är en cirkel med radien ett. I cirkeln finns en
vinkel inritad, (den röda tårtbiten). Vid vanliga mätningar av
vinklar med gradskiva anväder man oftast enheten grader, där ett
varv i cirkeln är 360 grader. Vi ska dock använda en annan enhet,
radianer. Ett varv i cirkeln är då 2*Pi radianer,
(Pi=3,141592654...). Funktionen sinus beräknar y-värdet för
cirkeln vid en given vinkel. Eftersom cirkeln är rund och har
radien ett kommer vi att få en kurva som pendlar mellan 1 och -1.
Det finns en motsvarande funktion för x-koordinaten som heter cosinus.

v = 0
do
v = v + 0.1
x = v * 10
y = sin(v) * 30 + 30
plot(x, y)
loop
Förskjutningen i cosinus beror på att x-värdet för cirkeln vid
vinkeln 0 är 1 medan y-värdet är 0. Vi skapar nu en loop där
vi låter vinkeln, v, starta
vid 0 och sedan ökas med 0,1 för varje varv. Vi lägger till en
funktion som ritar ut en punkt vid x = v * 10 och
y = sin(v) * 30 + 30, det vill säga x-koordinaten kommer
att öka med ett steg för varje varv och y-koordinaten kommer att
rita ut en sinus-kurva med amplitud (höjd) 60, (orginalkurvan
går ju mellan -1 och 1, vi multiplicerar detta med 30 och adderar
30 så att vi får en kurva mellan 0 och 60). Siffran 30 är helt godtycklig, exakt vilken amplitud man vill ha
på kurvan beror på vad man har för upplösning och vad man ska ha kurvan till. Genom att
kombinera sinus och cosinus på olika sätt kan man få till många
olika kurvor. Nedan finns några exempel. Samtliga
figurer nedan är konstruerade på liknande sätt som exemplet ovan.
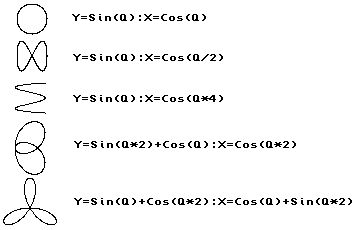
Kurvorna som vi skapar med dessa funktioner kan användas för
att bygga upp och rotera tredimentionella objekt. Till exempel kan
vi tänka oss att vi placerar hörnen i en kvadrat som fyra punkter på
cirkeln och drar linjer mellan hörnen. Genom att ändra vinkeln på
samma sätt som tidigare kan vi få kvadraten att rotera.
Tillbaka till indexet |